엘보우 방법(elbow method)와 실루엣 그래프(silhouette plot)
비지도 학습은 최종 답을 모르기 때문에 데이터 셋에 진짜 클래스 레이블이 없어서 지도학습의 성능 평가를 위한 기법들을 적용할 수 없다.
군집을 평가하기 위해서는 알고리즘 자체의 지표를 사용해야 한다.
k-means의 경우 성능을 평가하기 위해서 클래스 내 SSE(왜곡)을 사용한다.
km.inertia_속성에 계산되어 있다.
print('왜곡: %.2f' %km.inertia_)
왜곡: 72.48
엘보우 방법(elbow method)
엘보우 방법이라는 그래프를 사용하면, 문제에 최적인 클러스터 개수 k를 추정할 수 있다.
일반적으로 k가 증가하면, 왜곡이 줄어든다.(샘플이 할당된 센트로이드에 더 가까워 질 것임)
엘보우 방법은 이에서 빠르게 증가하는 지점의 k를 찾는 방법이다.
import matplotlib.plyplot as plt
from sklearn.cluster import KMeans
distortions=[]
for i in range(1, 11):
km=KMeans(n_clusters=i, init='k-means++', n_init=10, max_iter=300, random_state=0)
km.fit(X)
distortions.append(km.inertia_)
plt.plot(range(1, 11), distortions, marker='o')
plt.xlabel('Number of cluster')
plt.ylabel('Distortion')
plt.tight_layout()
plt.show()
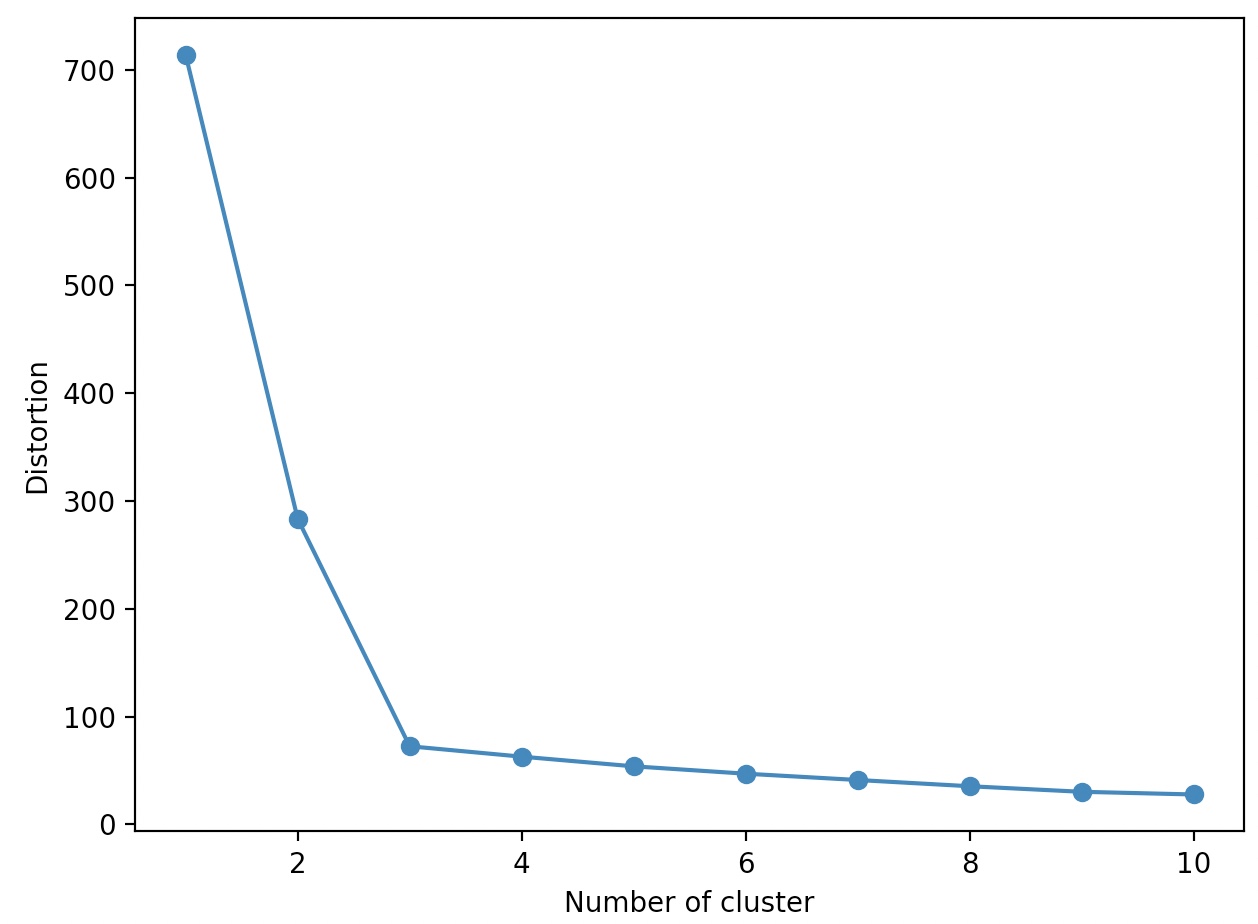
k=3에서 엘보우가 나타난다.
따라서 이 데이터셋에서는 k=3이 적절한 선택임을 알 수 있다.
이를 엘보우 방법이라고 한다.
실루엣 분석(silhoutette analysis)
실루엣 분석은 k-평균 알고리즘 이외에도 다른 군집 알고리즘에도 적용할 수 있는 평가 기법이다.
클러스터 내에 샘플들이 얼마나 조밀하게 모여 있는지를 측정하는 그래프 도구이다.
실루엣 계수 측정 Procsess
1. 샘플 x와 동일한 클러스터 내 모든 다른 포인트 사이의 거리를 평균하여 클러스터 응집력(cluster cohesion) a를 계산한다.![Python] K-means를 통한 기업 패턴 분류](resources/5A9DE740B4CF231755795CA0AB6F146D.png)
2. 샘플 x와 가장 가까운 클러스터의 모든 샘플 간 평균 거리로 최근접 클러스터의 클러스터 분리도(cluster separation) b를 계산한다.
3. 클러스터 응집력과 분리도 사이의 차이를 둘 중 큰 값으로 나누어 실루엣 s를 다음과 같이 계산한다.
클러스터 응집력과 클러스터 분리도가 같으면, 실루엣 계수가 0이 된다.
b>>a이면 가장 이상적이며, 실루엣 계수가 1에 가까워 진다.
실루엣 계수는 sklearn.metrics의 silhoutette_samples 함수로 계산 할 수 있다.
silhouteete_scores 함수는 모든 샘플에 걸쳐 평균 실루엣 계수를 계산한다.
silhoutette_scores==numpy.mean(silhouette_samples(…))
km=KMeans(n_clusters=3, init='k-means++', n_init=10, max_iter=300, tol=1e-04, random_state=0)
y_km=km.fit_predict(X)
import numpy as np
from matplotlib import cm
import matplotlib.pyplot as plt
from sklearn.metrics import silhouette_samples
cluster_labels=np.unique(y_km)
n_clusters=cluster_labels.shape[0]
silhouette_vals=silhouette_samples(X, y_km, metric='euclidean')
y_ax_lower, y_ax_upper=0, 0
yticks=[]
for i, c in enumerate(cluster_labels):
c_silhouette_vals=silhouette_vals[y_km==c]
c_silhouette_vals.sort()
y_ax_upper+=len(c_silhouette_vals)
color=cm.jet(float(i)/n_clusters)
plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height=1.0, edgecolor='none', color=color)
yticks.append((y_ax_lower+y_ax_upper)/2.)
y_ax_lower+=len(c_silhouette_vals)
silhouette_avg=np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color='red', linestyle='--')
plt.yticks(yticks, cluster_labels+1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.tight_layout()
plt.show()
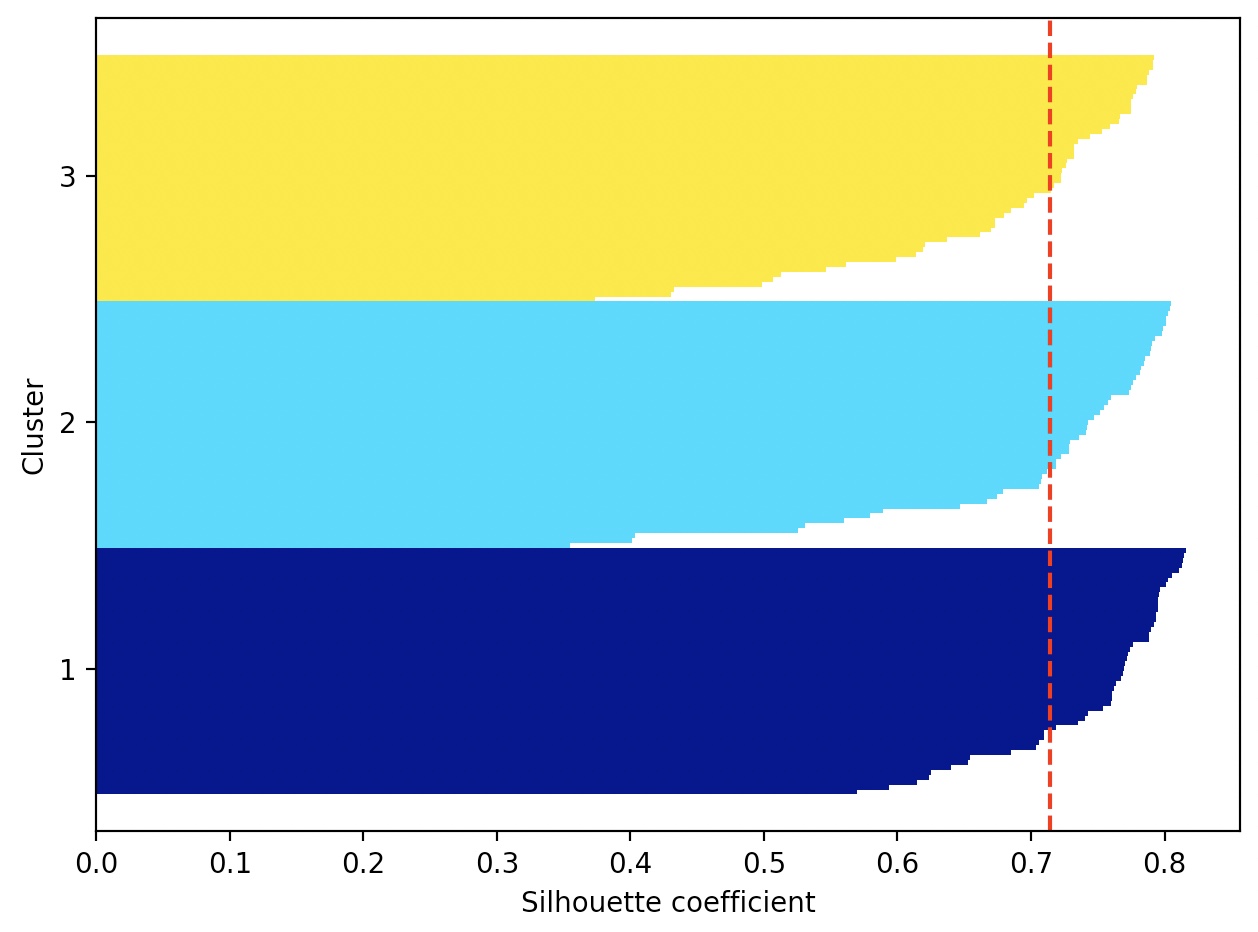
나쁜 군집에 대한 실루엣 그래프(두 개의 센트로이드로 k-means 알고리즘 적용)
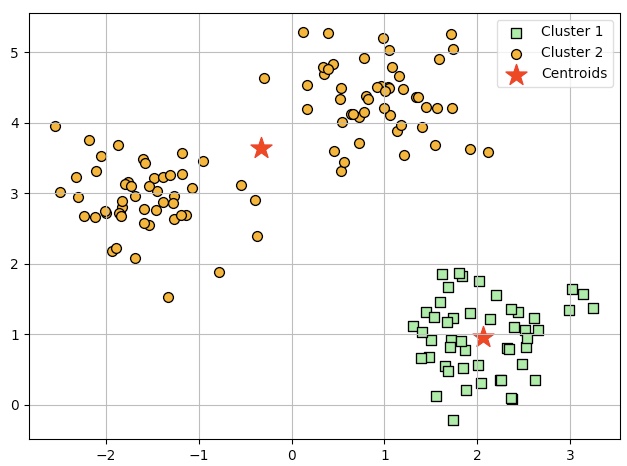
km=KMeans(n_clusters=2, init='k-means++', n_init=10, max_iter=300, tol=1e-04, random_state=0)
y_km=km.fit_predict(X)
plt.scatter(X[y_km==0, 0], X[y_km==0, 1], s=50, c='lightgreen', edgecolor='black', marker='s', label='Cluster 1')
plt.scatter(X[y_km==1, 0], X[y_km==1, 1], s=50, c='orange', edgecolor='black', marker='o', label='Cluster 2')
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1], s=250, marker='*', c='red', label='Centroids')
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()
cluster_labels=np.unique(y_km)
n_clusters=cluster_labels.shape[0]
silhouette_vals=silhouette_samples(X, y_km, metric='euclidean')
y_ax_lower, y_ax_upper=0, 0
yticks=[]
for i, c in enumerate(cluster_labels):
c_silhouette_vals=silhouette_vals[y_km==c]
c_silhouette_vals.sort()
y_ax_upper+=len(c_silhouette_vals)
color=cm.jet(i/n_clusters)
plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height=1.0, edgecolor='none', color=color)
yticks.append((y_ax_lower+y_ax_upper)/2)
y_ax_lower+=len(c_silhouette_vals)
silhouette_avg=np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color='red', linestyle='--')
plt.yticks(yticks, cluster_labels+1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.tight_layout()
plt.show()
두 개의 길이와 두께가 확연히 다르다.
이는 군집 결과가 나쁘거나, 적어도 최적은 아니라는 증거이다.